一、组合计数中的基本概念与性质
1、排列
定义
一般地,从n个不同元素中取出$m(m\leqslant n)$个元素,按照一定的顺序排成一列,叫做从$n$个元素中取出$m$个元素的一个排列
特别地,当$m=n$时,这个排列被称作全排列,记作$A_n^m$
性质
$A_n^m=\frac{n!}{(n-m)!}$
证明:第一个数有$n$种选择,第二个数有$n-1$种选择,……,第$m$个数有$n-m+1$
$\therefore A_n^m=\prod \limits_{i=n}^{n-m+1}i=\frac{n!}{(n-m)!}$
2、组合
定义
从$n$个不同的元素中,任取$m(m\leqslant n)$个元素为一组,叫作从$n$个不同元素中取出$m$个元素的一个组合,记作$C_n^m$或$\binom{n}{m}$
性质
①$\binom{n}{m}=\frac{n!}{m!(n-m)!}$
证明:先从从$n$个元素中取出$m$个元素的一个排列,有$A^m_n$种取法,再把所有排列中的数排序,有$A^m_m$个是重复的
$\therefore \binom{n}{m}=\frac{A^m_n}{A^m_m}=\frac{n!}{m!(n-m)!}$
②$\binom{n}{m}=\binom{n}{n-m}$
证明(数学法):$\binom{n}{m}=\frac{n!}{m!(n-m)!}=\frac{n!}{(n-m)!(n-(n-m))!}=\binom{n}{n-m}$
证明(讲故事法):从前,有一个班级有$n$个小朋友,老师要从中选$m$个小朋友扫地,共有$\binom{n}{m}$种方法,相当于从中选出$n-m$个小朋友不扫地,有$\binom{n}{n-m}$种方法
$\therefore \binom{n}{m}=\binom{n}{n-m}$多么精彩的故事啊!此处应有掌声
③$\binom{n}{m}=\binom{n-1}{m-1}+\binom{n-1}{m}$
证明(数学法):$\binom{n}{m}=\frac{n!}{m!(n-m)!}=\frac{m}{n}\times \frac{n!}{m!(n-m)!}+\frac{n-m}{n}\times \frac{n!}{m!(n-m)!}=\frac{(n-1)!}{(m-1)!(n-m)!}+\frac{(n-1)!}{m!(n-m-1)!}=\binom{n-1}{m-1}+\binom{n-1}{m}$
证明(讲故事法):从前,有一个班级有$n$个小朋友,老师要从中选$m$个小朋友扫地,共有$\binom{n}{m}$种方法。也可以先决定$1$号小朋友选不选,如果选,就在剩下的$n-1$个小朋友中选出$m-1$个小朋友扫地,有$\binom{n-1}{m-1}$种方法;如果不选,就在剩下的$n-1$个小朋友中选出$m$个小朋友扫地,有$\binom{n-1}{m}$种方法,一共$\binom{n-1}{m-1}+\binom{n-1}{m}$种方法
$\therefore \binom{n}{m}=\binom{n-1}{m-1}+\binom{n-1}{m}$多么精彩的故事啊!此处应有掌声
④$m\binom{n}{m}=n\binom{n-1}{m-1}$
证明(数学法):$m\binom{n}{m}=m\times \frac{n!}{m!(n-m)!}=\frac{n!}{(m-1)!(n-m)!}=n\times \frac{(n-1)!}{(m-1)!(n-1-(m-1))!}=n\binom{n-1}{m-1}$
证明(讲故事法):从前,有一个班级有$n$个小朋友,老师要从中选$m$个小朋友扫地再选出一个人担任扫地长(???),共有$m\binom{n}{m}$种方法。也可以先选一个扫地长,再在剩下的$n-1$个小朋友中选出$m-1$个小朋友扫地,有$n\binom{n-1}{m-1}$种方法
$\therefore m\binom{n}{m}=n\binom{n-1}{m-1}$多么精彩的故事啊!此处应有掌声
⑤$\sum \limits_{i=0}^n\binom{n}{i}=2^n$
证明(数学法):$\sum \limits_{i=0}^n\binom{n}{i}=\sum \limits_{i=0}^n\binom{n}{i}\times 1^i\times 1^{n-i}=(1+1)^n=2^n$
证明(讲故事法):从前,有一个班级有$n$个小朋友,老师要从中选若干个小朋友扫地,共有$\sum \limits_{i=0}^n\binom{n}{i}$种方法。也可以先决定$1$号小朋友选不选,有$2$种方法,再决定$2$号小朋友选不选,也有$2$种方法……最后决定$n$号小朋友选不选,还是有$2$种方法,有$2^n$种方法
$\sum \limits_{i=0}^n\binom{n}{i}=2^n$多么精彩的故事啊!此处应有掌声
我写的所谓的“讲故事法”在证明组合恒等式的时候非常的有用但是这里不讲,主要的难度就是在于故事是什么,剩下的就没有什么难度了
二、组合计数中的一些常用技巧
1、容斥原理
定义
先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复
这种计数的方法称为容斥原理
公式
$\left|\bigcup \limits_{i=1}^nA_i\right|=\sum \limits_{k=1}^n(-1)^{k-1}\sum \limits_{0<i_1<i_2<\cdots<i_k\leqslant n}\left|\bigcap \limits_{i=1}^kA_{i_k}\right|$
我觉得这个结论很显然,举个例子,当$n=3$时,我们可以画一个VanVenn图: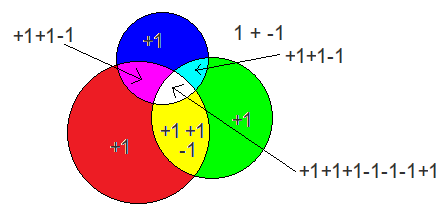
我不会严格证明,但是度娘上有,可以自己看
2、捆绑与插空法
这是啥?
这两种方法是用来解决排列时两个人要求不能在一起或者必须在一起的问题
捆绑法
考虑这样一个问题:有$n$个人排队,其中有两个人一定要排在一起,问有几种排法
显然,我们可以考虑把这两个人绑在一起,将他们合并为一个人
所以相当于是$n-1$个人排队,最后记得考虑两个人内部的顺序,共$2(n-1)!$种
插空法
考虑这样一个问题:有$n$个人排队,其中有两个人一定不排在一起,问有几种排法
上面是合并,现在呢?我们先把剩下的$n-2$个人排好序,留出$n-1$个空位,然后把这两个人塞到空位里去就完事了,共$(n-2)!(n-1)(n-2)$种
3、隔板法
组合计数中在生成函数以前及其重要的方法之一,延伸出去,就是斯特林数以及正整数的拆分问题
考虑这样一个问题:有$n$个相同的球,$k$个不同的盒子,把$n$个球放到盒子里,盒子不允许为空,有多少种方案
如何计数呢?很简单,我们把$n$个球排成一行,在中间放上$k-1$块板
接着,我们把第$i-1$块板和第$i$块板之间的球放到第$i$个盒子中就完了
所以答案就是$\binom{n-1}{k-1}$
是不是很简单?
那么下一个问题:求不定方程$x_1+x_2+\cdots \cdots x_k=n$($x_i$为正整数)的解的个数
聪明的你一定会发现,这个问题和上面的问题一毛一样
接着,下一个问题:有$n$个相同的球,$k$个不同的盒子,把$n$个球放到盒子里,盒子允许为空,有多少种方案
这怎么处理?我们考虑一种转化的思路
这个问题相当于:求不定方程$x_1+x_2+\cdots \cdots x_k=n$($x_i$为自然数)的解的个数
所以,我们设$y_i=x_i+1$,则问题转化为求不定方程$y_1+y_2+\cdots \cdots y_k=n+k$($x_i$为正整数)的解的个数
因此,答案就是$\binom{n+k-1}{k-1}$
这就是基础的组合计数常用的概念和方法了,至于练习,建议做《数学奥林匹克竞赛小丛书》里的内容