~~第一次当标题党好方，但好像也没啥问题，因为我就是一个初中的菜鸡~~

前置知识

基础的组合计数知识
NTT（非必要）
看到一长串的式子不会晕过去的能力
盒放球
盒放球问题可以描述为：

有$n$个相同/不同的球，$k$个相同/不同的盒子，把$n$个球放到盒子里，盒子允许/不允许为空，有多少种方案

稍微有点智商的人都知道，这一共有$2\times2\times2=8$个问题
我们一个个来看

球相同，盒不同，不允许为空

这个非常简单，只需要使用隔板法就可以了，在$n-1$个空中插入$k-1$个板，把球隔成$k$段，每一段对应地放到盒子中，所以有$\binom{n-1}{k-1}$种

球相同，盒不同，允许为空

这回变成了允许为空，怎么办？
很简单，先在每个盒子里都放一个球，这样就转化为了球相同，盒不同，不允许为空的情况了！一共有$\binom{n+k-1}{k-1}$

球相同，盒相同，不允许/允许为空

这个需要使用到母函数（生成函数），不是本篇文章的重点，所以先不讲

球不同，盒不同，允许为空

这个应该没人不会吧……当然是$k^n$种了

球不同，盒相同，不允许为空

emmm……
这是一个很有难度的问题，我们先看看如何递推吧
假设有$S(n,k)$种，那么可能是前$n-1$个球就用了$k$个盒子，那么我们把第$n$个球放在$k$个盒子中的任意一个即可；如果前$n-1$个球用了$k-1$个盒子，那么我们就把第$n$个球放在第$k$个盒子中
所以$S(n,k)=S(n-1,k)\times k+S(n-1,k-1)$
话说我们不是要斯特林数吗？怎么还没讲？
别急，看看这个问题所使用的的字母：$S$，好像跟斯特林的首字母一样
不会吧不会吧，难道这就是传说中的斯特林数，原来斯特林数这么简单！！！~~对，您太强了，所以觉得简单，可以爆踩我这个菜鸡，妈妈再也不用担心你的学习啦！（大雾~~
接下来，我们暂且放下剩下的两种盒放球问题，来看看我们刚刚计算的$S(n,k)$，也就是第二类斯特林数的定义

第二类斯特林数

定义

将$n$个元素分成$m$个无标号的集合$S(n,m)=\begin{Bmatrix}n\\m\end{Bmatrix}$
等等，啥叫无标号集合啊？如果用上面的盒放球问题来解释，就是盒子是相同的，如果严谨一点说，就是如果一堆集合调换顺序后和另一堆集合完全相同（所有对应的集合都相等），那么这两堆集合就是等价的
比如$\{\{1\},\{2,3\}\}$和$\{\{2,3\},\{1\}\}$就是等价的
看到这里，相信有的人还是理解不了第二类斯特林数，所以，我们举一个例子：$\begin{Bmatrix}3\\2\end{Bmatrix}=3$
三种方法如下：

$\{\{1\},\{2,3\}\}$
$\{\{2\},\{1,3\}\}$
$\{\{3\},\{1,2\}\}$

现在清楚多了吧？

通项

第二类斯特林数的通项为$\begin{Bmatrix}n\\m\end{Bmatrix}=\frac{1}{m!}\sum \limits_{i=0}^m(-1)^i\binom{m}{i}(m-i)^n$
可以通过盒放球问题，来感性理解这个公式：我们考虑容斥，假设有$i$个空盒，那么，我们先从$m$个盒子中，选出$i$个，剩下的盒子随便塞
最后，不要忘记无标号这个问题，所以我们需要除以$m!$
这个公式非常重要，它可以帮助我们用NTT计算出一整行的第二类斯特林数，这个后面会讲到

特殊值

在开始讲NTT求第二类斯特林数之前，为了让大家放松心情，我们先来看看第二类斯特林数的特殊值：
$\begin{Bmatrix}n\\0\end{Bmatrix}=0,\begin{Bmatrix}n\\1\end{Bmatrix}=1,\begin{Bmatrix}n\\n-1\end{Bmatrix}=\binom{n}{2},\begin{Bmatrix}n\\n\end{Bmatrix}=1$
自己想吧，太简单了，不证了

计算第二类斯特林数

Warning!Warning!Warning!前方高能，请没学过NTT迅速跳过这一节
好的，我们开始推式子吧！
$\begin{Bmatrix}n\\m\end{Bmatrix}=\frac{1}{m!}\sum \limits_{i=0}^m(-1)^i\binom{m}{i}(m-i)^n=\frac{1}{m!}\sum \limits_{i=0}^m(-1)^i\frac{m!}{i!(m-i)!}(m-i)^n=\sum \limits_{i=0}^m\frac{(-1)^i}{i!}\frac{(m-i)^n}{(m-i)!}$
看，这是什么？是不是一个漂亮的卷积式？
还没看出来？设$f(x)=\sum \limits_{i\geqslant 0} \frac{(-1)^i}{i!}x^i,g(x)=\sum\limits_{i\geqslant 0}\frac{i^n}{i!}x^i$，则$\begin{Bmatrix}n\\m\end{Bmatrix}$就是$f(x)$和$g(x)$的卷积
所以，我们就可以愉快地使用逆天塔（NTT）了！
模板题代码：

#include<bits/stdc++.h>
#define ljc 167772161
#define int long long
#define ll long long
using namespace std;
int n,m,k,r[800006],lim,w[800006],a[800006],b[800006],inv[800006];
inline ll fast_pow(ll a,ll b,ll p){
    ll t=1;a%=p;
    while (b){
        if (b&1) t=t*a%p;
        b>>=1;a=a*a%p;
    }
    return t;
}
inline void NTT(ll f[],int lim,int id){
    for (int i=0;i<lim;i++){
        if (i<r[i]) swap(f[r[i]],f[i]);
    }
    w[0]=1;
    for (int len=1;len<lim;len<<=1){
        ll gen=fast_pow(3,(ljc-1)/(len<<1)*id+ljc-1,ljc);
        for (int i=1;i<len;i++) w[i]=w[i-1]*gen%ljc;
        for (int i=0;i<lim;i+=len<<1){
            ll *f1=f+i,*f2=f1+len;
            for (int j=0;j<len;j++){
                ll x=f1[j]%ljc,y=f2[j]*w[j]%ljc;
                f1[j]=(x+y)%ljc;f2[j]=(x-y+ljc)%ljc;
            }
        }
    }
    if (id==1) return;
    ll Inv=fast_pow(lim,ljc-2,ljc);
    for (int i=0;i<lim;i++) f[i]=f[i]*Inv%ljc;
}
signed main(){
    cin>>n;n++;
    inv[0]=inv[1]=1;
    for (int i=2;i<n;i++) inv[i]=(ljc-(ljc/i)*inv[ljc%i]%ljc)%ljc;
    for (int i=1;i<n;i++) inv[i]=inv[i-1]*inv[i]%ljc;
    for (int i=0,one=1;i<n;one=ljc-one,i++){
        a[i]=one*inv[i]%ljc;b[i]=fast_pow(i,n-1,ljc)*inv[i]%ljc;
    }
    int lim=1,len=0;
    while (lim<=(n<<1)) lim<<=1,len++;
    for (int i=0;i<lim;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(len-1));
    NTT(a,lim,1);NTT(b,lim,1);
    for (int i=0;i<lim;i++) a[i]=a[i]*b[i]%ljc;
    NTT(a,lim,-1);
    for (int i=0;i<n;i++) printf("%lld ",a[i]);
}

自然数幂和

你有没有见过这样的题目：让你求$\sum\limits_{i=1}^ni^k$的题目？
你可能会想：这不简单吗，每次使用快速幂不就好了嘛
不！没有那么简单！$n\leqslant 10^9,k\leqslant 5000$的时候你还能用快速幂吗？不能！~~不要告诉我你要分段打表~~
但是！第二类斯特林数可以！
这只能说明：斯特林数（停顿）行！快速幂（停顿）不行！我爱斯特林数！~~老伏拉夫了~~
那斯特林数到底怎么行了呢？我们要从一个假快速幂讲起

快速幂？

$n^m=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}$
其中$n^{\underline{i}}$表示$n$的$i$次下降幂，即$n^{\underline{i}}=\prod \limits_{k=0}^{i-1}(n-k)$
证明：
考虑归纳证明，当$m=1$时，$\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}=\begin{Bmatrix}1\\1\end{Bmatrix} n=n$
假设$m=k$时成立
当$m=k+1$时，$n^{k+1}=n\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix} n^{\underline{i}}=\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix}\left( n^{\underline{i+1}}+in^{\underline{i}}\right)=\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix} n^{\underline{i+1}}+\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix} in^{\underline{i}}=\sum \limits_{i=0}^{k+1} \begin{Bmatrix}k\\i-1\end{Bmatrix} n^{\underline{i}}+\sum \limits_{i=0}^{k+1} \begin{Bmatrix}k\\i\end{Bmatrix} in^{\underline{i}}=\sum \limits_{i=0}^{k+1} \left(\begin{Bmatrix}k\\i-1\end{Bmatrix}+i\begin{Bmatrix}k\\i\end{Bmatrix}\right) n^{\underline{i}}=\sum \limits_{i=0}^{k+1} \begin{Bmatrix}k+1\\i\end{Bmatrix} n^{\underline{i}}$
$\therefore n^m=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}$

解决自然数幂和问题

设$S_{n,k}=\sum\limits_{i=1}^ni^k$
$S_{n,k}=\sum\limits_{i=1}^ni^k=\sum\limits_{i=1}^n\sum \limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix} i^{\underline{j}}$
考虑到$n$的范围太大，$k$的范围小，交换求和顺序
$=\sum \limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix}\sum\limits_{i=1}^ni^{\underline{j}}=\sum \limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix}j!\sum\limits_{i=1}^n\binom{i}{j}=\sum \limits_{j=0}^{k} \begin{Bmatrix}k\\j\end{Bmatrix}j!\binom{n+1}{j+1}$
斯特林数预处理，组合数和阶乘边算边推，所以效率就是$\Theta(k)$！

再次证明了我说的话：斯特林数行！快速幂不行！我爱斯特林数！

第一类斯特林数

既然刚刚讲了第二类斯特林数，一定有第一类斯特林数吧？
有！接下来我们就来讲讲

定义

将$n$个元素分成$m$个无标号的轮换$s(n,m)=\begin{bmatrix}n\\m\end{bmatrix}$
什么叫轮换？
就是把一堆数放在一个圈上，如果可以通过旋转使得圈上的每个位置上数都和另一个圈上的数是相等的，那么这两个圈等价（意思就是它们是同一个轮换）
比如，现在有三个轮换：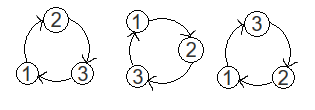

第一个轮换和第二个轮换是等价的，第一个和第三个轮换不是等价的
那么，什么叫无标号的轮换？
和无标号的集合类似，就是如果一堆轮换调换顺序后和另一堆轮换完全相同（所有对应的轮换等价），那么这两堆轮换就是等价的
比如，现在有两堆轮换：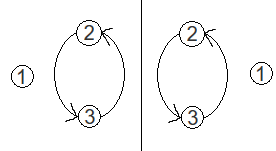

第一堆轮换和第二堆轮换完全相同，是等价的
为了让大家更了解第一类斯特林数，我们举一个例子：$\begin{bmatrix}3\\2\end{bmatrix}=3$
三种方法如下：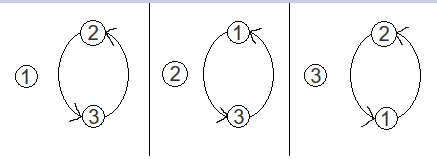

第一类斯特林数还有另一种定义，就是$\prod \limits_{i=0}^{n-1}(x-i)$的$m$次项系数叫$\begin{bmatrix}n\\m\end{bmatrix}$
因为我太菜了，所以我并不知道第一类斯特林数是否有通项

特殊值

$\begin{bmatrix}n\\0\end{bmatrix}=0,\begin{bmatrix}n\\1\end{bmatrix}=1,\begin{bmatrix}n\\n-1\end{bmatrix}=\binom{n}{2},\begin{bmatrix}n\\n\end{bmatrix}=1$
自己想吧，太简单了，不证了

快速幂？

和第二类斯特林数一样，第一类斯特林数也有假的快速幂，还有两个：
①$n^{\overline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} n^i$
其中$n^{\overline{m}}$表示$n$的$i$次上升幂，即$n^{\overline{m}}=\prod \limits_{i=0}^{m-1}(n+i)$
证明：
当$m=1$时，$\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} n^i=\begin{bmatrix}1\\1\end{bmatrix} n=n$
假设$m=k$时成立
当$m=k+1$时，$n^{\overline{k+1}}=(n+k)n^{\overline{k}}=n\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} n^i+k\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k\\i-1\end{bmatrix} n^i+\sum \limits_{i=0}^{k+1} k\begin{bmatrix}k\\i\end{bmatrix} n^i=\sum \limits_{i=0}^{k+1} \left(\begin{bmatrix}k\\i-1\end{bmatrix}+k\begin{bmatrix}k\\i\end{bmatrix}\right) n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k+1\\i\end{bmatrix} n^i$
$\therefore n^{\overline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} n^i$
②$n^{\underline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} (-1)^{m-i} n^i$
证明：
当$m=1$时，$\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} (-1)^{m-i} n^i=\begin{bmatrix}1\\1\end{bmatrix} n=n$
假设$m=k$时成立
当$m=k+1$时，$n^{\underline{k+1}}=(n-k)n^{\underline{k}}=n\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} (-1)^{k-i} n^i-k\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} (-1)^{k-i} n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k\\i-1\end{bmatrix} (-1)^{k+1-i} n^i+\sum \limits_{i=0}^{k+1} k\begin{bmatrix}k\\i\end{bmatrix} (-1)^{k+1-i} n^i=\sum \limits_{i=0}^{k+1} \left(\begin{bmatrix}k\\i-1\end{bmatrix}+k\begin{bmatrix}k\\i\end{bmatrix}\right) (-1)^{k+1-i} n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k+1\\i\end{bmatrix} (-1)^{k+1-i} n^i$
$\therefore n^{\underline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} (-1)^{m-i} n^i$
通过第一个假快速幂，我们可以用分治NTT，求出第一类斯特林数，但是我太菜了，不会，等会了再来更博吧

斯特林反演

最后我们来讲讲斯特林反演
若$f(n)=\sum \limits_{i=1}^n\begin{Bmatrix}n\\i\end{Bmatrix}g(i)$，则$g(n)=\sum \limits_{i=1}^n(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}f(i)$
这个$-1$的次数怎么这么熟？
是的，这就是上面的第一类斯特林数的第二个假快速幂中$-1$次数
可以用斯特林反演说明第二类斯特林数的假快速幂和第一类斯特林数的第二个假快速幂是等价的
但是这玩意儿好像没啥用，至少我没用过~~我就没做过几道斯特林数的题目~~，但是我还是来证一下

引理1

引理描述：$x^{\underline{n}}=(-1)^n(-x)^{\overline{n}},x^{\overline{n}}=(-1)^n(-x)^{\underline{n}}$
引理证明：$(-1)^n(-x)^{\overline{n}}=\sum\limits_{i=0}^{i=n-1} (-1)\times(-x+i)=\sum\limits_{i=0}^{i=n-1} (x-i)=x^{\underline{n}}$
$\therefore (-1)^n(-x)^{\underline{n}}=(-1)^{2n}x^{\overline{n}}=x^{\overline{n}}$

引理2

引理描述：$\sum\limits_{i=m}^{n}(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}\begin{Bmatrix}i\\m\end{Bmatrix}=[n==m],\sum\limits_{i=m}^{n}(-1)^{n-i}\begin{Bmatrix}n\\i\end{Bmatrix}\begin{bmatrix}i\\m\end{bmatrix}=[n==m]$
引理证明：$n^m=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} (-1)^i (-n)^{\overline{i}}=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} (-1)^i\sum \limits_{j=0}^{i} \begin{bmatrix}i\\j\end{bmatrix} (-n)^j=\sum \limits_{j=0}^{m}n^j \sum \limits_{i=j}^{m} \begin{Bmatrix}m\\i\end{Bmatrix}\begin{bmatrix}i\\j\end{bmatrix} (-1)^{i-j}$
$\therefore \sum \limits_{i=j}^{m} \begin{Bmatrix}m\\i\end{Bmatrix}\begin{bmatrix}i\\j\end{bmatrix} (-1)^{i-j}=[j==m]$
$\therefore \sum\limits_{i=m}^{n}(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}\begin{Bmatrix}i\\m\end{Bmatrix}=[n==m]$
同理可证，$\sum\limits_{i=m}^{n}(-1)^{n-i}\begin{Bmatrix}n\\i\end{Bmatrix}\begin{bmatrix}i\\m\end{bmatrix}=[n==m]$

斯特林反演证明

斯特林反演命题描述：若$f(n)=\sum \limits_{i=1}^n\begin{Bmatrix}n\\i\end{Bmatrix}g(i)$，则$g(n)=\sum \limits_{i=1}^n(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}f(i)$
证明：$g(n)=\sum\limits_{i=0}^n [i==n]g(i)=\sum\limits_{i=0}^{n}\sum\limits_{j=i}^{n}(-1)^{n-j}\begin{bmatrix}n\\j\end{bmatrix}\begin{Bmatrix}j\\i\end{Bmatrix}g(i)=\sum \limits_{j=1}^n(-1)^{n-j}\begin{bmatrix}n\\j\end{bmatrix}\sum \limits_{i=0}^j\begin{Bmatrix}j\\i\end{Bmatrix}g(i)=\sum \limits_{j=1}^n(-1)^{n-j}\begin{bmatrix}n\\j\end{bmatrix}f(j)$

例题详解

第一类斯特林数

[FJOI2016]建筑师

题目

题目链接

题解

显然，这个建筑群一定会呈现这个样子：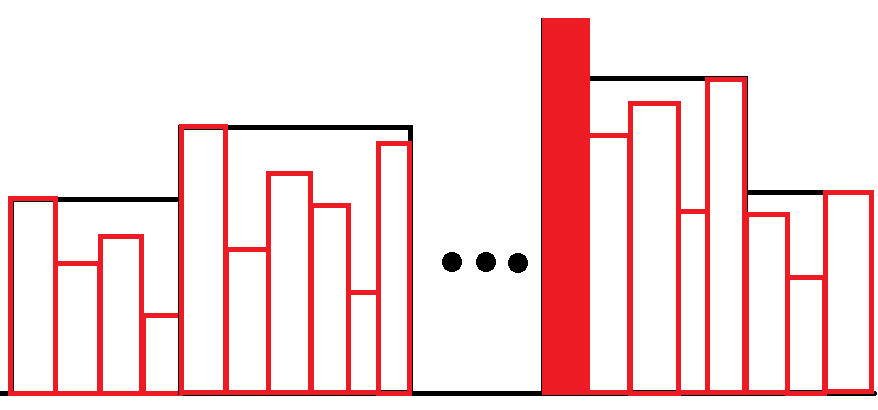

其中，红色的代表一栋建筑，黑色的框代表一个建筑块（？？？），填充为红色的建筑高为$n$
去掉这个最高的建筑，剩下的建筑就一定被分成了$A+B-2$个块，其中左边有$A-1$个，右边有$B-1$个
这是因为每个建筑块有且仅有一个建筑能被看见（这是显然的吧……感性理解一下）
研究一下每一个建筑块会发现，对于一个一共有$k$个建筑的建筑块，当最高的建筑已经被选出时，这个建筑块一共有$(k-1)!$种方案
这让我们想到了单独一个环的排列也是$(k-1)!$种！
所以这岂不是第一类斯特林数？
最后，我们就会知道，答案是$\binom{A+B-2}{A-1}\begin{bmatrix}n-1\\A+B-2\end{bmatrix}$
附上代码：

#include<iostream>
using namespace std;
int n,a,b,MOD=1e9+7,s[50010][210],c[210][210];
int main()
{
    s[0][0]=c[0][0]=1;
    for(int i=1;i<=50000;i++) for(int j=1;j<=min(i,200);j++) s[i][j]=(1ll*s[i-1][j]*(i-1)%MOD+s[i-1][j-1])%MOD;
    for(int i=1;i<=200;i++){
        c[i][0]=c[i][i]=1;
        for(int j=1;j<i;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%MOD;
    }
    int T;
    cin>>T;
    while(T--) cin>>n>>a>>b,cout<<1ll*s[n-1][a+b-2]*c[a+b-2][a-1]%MOD<<endl;
}

其他练习题

洛谷P5408 第一类斯特林数·行

CF960G Bandit Blues

第二类斯特林数

[省选联考 2020 A 卷] 组合数问题

题目

题目链接

题解

$\sum\limits_{i=0}^ma_i\sum \limits_{k=0}^nx^k\binom{n}{k}k^i=\sum\limits_{i=0}^ma_i\sum \limits_{k=0}^nx^k\binom{n}{k}\sum\limits_{j=1}^ik^{\underline{j}}\begin{Bmatrix}i\\j\end{Bmatrix}=\sum\limits_{i=0}^ma_i\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}\sum \limits_{k=0}^nx^k\binom{n}{k}k^{\underline{j}}=\sum\limits_{i=0}^ma_i\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}\sum \limits_{k=0}^nx^k\binom{n}{k}j!\binom{k}{j}=\sum\limits_{i=0}^ma_i\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}j!\sum \limits_{k=0}^nx^k\binom{n}{k}\binom{k}{j}=\sum\limits_{i=0}^ma_i\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}j!\sum \limits_{k=0}^nx^k\binom{n}{j}\binom{n-j}{k-j}=\sum\limits_{i=0}^ma_i\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}j!\binom{n}{j}\sum \limits_{k=0}^{n-j}x^{k+j}\binom{n-j}{k}=\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}j!\binom{n}{j}x^j\sum \limits_{k=0}^{n-j}x^k\binom{n-j}{k}=\sum\limits_{j=1}^i\begin{Bmatrix}i\\j\end{Bmatrix}j!\binom{n}{j}x^j(x+1)^{n-j}$

附上代码：

#include<cstdio>
using namespace std;
int n,x,MOD,m,ans,a[1010],sti[1010][1010];
int POW(int a,int b)
{
    int ans=1;
    for(;b;b>>=1){
        if(b&1) ans=(1ll*ans*a)%MOD;
        a=(1ll*a*a)%MOD;
    }
    return ans;
}
int main()
{
    scanf("%d%d%d%d",&n,&x,&MOD,&m),sti[1][1]=1;
    for(int i=0;i<=m;i++) scanf("%d",&a[i]);
    for(int i=2;i<=m;i++) for(int j=1;j<=i;j++) sti[i][j]=((1ll*sti[i-1][j]*j)%MOD+sti[i-1][j-1])%MOD;
    ans=(1ll*a[0]*POW((x+1)%MOD,n))%MOD;
    for(int i=1;i<=m;i++){
        int temp=(1ll*POW(x%MOD,i)*POW((x+1)%MOD,n-i))%MOD,sum=0;
        for(int j=0;j<=i-1;j++) temp=(1ll*temp*(n-j))%MOD;
        for(int j=i;j<=m;j++) (sum+=(1ll*sti[j][i]*a[j])%MOD)%=MOD;
        (ans+=(1ll*sum*temp)%MOD)%=MOD;
    }
    printf("%d",ans);
}

其他练习题

[HEOI2016/TJOI2016]求和

CF961G Partitions

自然数幂和

CF932E Team Work

题目

题目链接（洛谷）
题目链接（CF）

题解

$\sum\limits_{i=1}^n\binom{n}{i}i^k=\sum\limits_{i=1}^n\binom{n}{i}\sum\limits_{j=0}^i\binom{i}{j}\begin{Bmatrix}k\\j\end{Bmatrix}j!=\sum\limits_{i=1}^n\frac{n!}{(n-i)!}\sum\limits_{j=0}^i\frac{\begin{Bmatrix}k\\j\end{Bmatrix}}{(i-j)!}=\sum\limits_{j=1}^{min(n,k)}\begin{Bmatrix}k\\j\end{Bmatrix}\sum\limits_{i=j}^n\frac{n!}{(n-i)!(i-j)!}=\sum\limits_{j=1}^{min(n,k)}\begin{Bmatrix}k\\j\end{Bmatrix}\sum\limits_{i=j}^n\frac{n!}{(n-j)!}\frac{(n-j)!}{(n-i)!(i-j)!}=\sum\limits_{j=1}^{min(n,k)}\begin{Bmatrix}k\\j\end{Bmatrix}\frac{n!}{(n-j)!}\sum\limits_{i=j}^n\binom{n-j}{i-j}=\sum\limits_{j=1}^{min(n,k)}\begin{Bmatrix}k\\j\end{Bmatrix}\frac{n!}{(n-j)!}2^{n-j}$
斯特林数预处理，$2^{n-j}$用快速幂，$\frac{n!}{(n-j)!}$边推边算，效率$\Theta(k)$
附上代码：

#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
int n,k,t,mod=1e9+7,ans,sti[5010][5010],c[300010];
int POW(int a,int b)
{
    int ans=1;
    for(;b;b>>=1){
        if(b&1) ans=1ll*ans*a%mod;
        a=1ll*a*a%mod;
    }
    return ans;
}
int main()
{
    cin>>n>>k,t=min(n,k),sti[1][1]=1,c[0]=n;
    for(int i=2;i<=k;i++) for(int j=1;j<=min(n,i);j++) sti[i][j]=(1ll*sti[i-1][j]*j%mod+sti[i-1][j-1])%mod;
    for(int i=1;i<=t;i++) c[i]=1ll*c[i-1]*(n-i)%mod;
    for(int i=1;i<=t;i++) ans=(ans+1ll*c[i-1]%mod*sti[k][i]%mod*POW(2,n-i)%mod)%mod;
    cout<<ans;
}

对于这道题目，有一道升级版的题目叫做原题的价值，需要使用NTT（当然，这道题你也可以使用NTT三模数的方式书写，但是太复杂啦！），可是我并不知道哪里可以提交这道题目（我们学校的OJ上有）
另外说一句，自然数幂和也可以用第一类斯特林数$\Theta\left(k^2\right)$解决，只是比较复杂，这里就不讲了

初中生都看得懂的快速上手斯特林数指南--从盒放球问题说起

前置知识

盒放球

球相同，盒不同，不允许为空

球相同，盒不同，允许为空

球相同，盒相同，不允许/允许为空

球不同，盒不同，允许为空

球不同，盒相同，不允许为空

第二类斯特林数

定义

通项

特殊值

计算第二类斯特林数

自然数幂和

快速幂？

解决自然数幂和问题

第一类斯特林数

定义

特殊值

快速幂？

斯特林反演

引理1

引理2

斯特林反演证明

例题详解

第一类斯特林数

[FJOI2016]建筑师

题目

题解

其他练习题

第二类斯特林数

[省选联考 2020 A 卷] 组合数问题

题目

题解

其他练习题

自然数幂和

CF932E Team Work

题目

题解

相关练习题