DTOJ3312 行走

题目

题目描述

“我有个愿望，我希望走到你身边。”
这是个奇异的世界，世界上的$n-1$条路联结起来形成一棵树，每条路有一个对应的权值$c_i$（？？？）
现在我会给出$q$组询问或操作
每次询问我会从一个$x$点走到$y$点，初始在$x$点我会有一个数字$v$，然后每走过一条权值为$c$的边，我的$v$就会变成$\left\lfloor \frac{v}{c} \right\rfloor$ ,问最后到
$y$时$v$变成了什么
每次修改我会修改一条边的权值，保证修改后的权值小于等于原来的权值且不会小于$1$
每组询问或操作的格式如下：
询问：$1~x~y~v$表示从$x$走到$y$，一开始的数字为$v$
操作：$2~p~c$表示将第$p$条边的边权修改为$c$

输入格式

第一行两个整数$n$和$q$表示点个数和询问与操作个数
接下来$n-1$行每行三个整数$u,v,c$表示$u$与$v$之间有一条边权为$c$的边
接下来$q$行每行第一个数$type$
如果$type=1$那么接下来三个数$x,y,v$表示一组询问
如果$type=2$那么接下来两个数$p,c$表示一组操作

输出格式

对于每组询问输出一个数表示最后的答案

样例

样例输入

样例输入1

6 6
1 2 1
1 3 7
1 4 4
2 5 5
2 6 2
1 4 6 17
2 3 2
1 4 6 17
1 5 5 20
2 4 1
1 5 1 3

样例输入2

5 4
1 2 7
1 3 3
3 4 2
3 5 5
1 4 2 100
1 5 4 1
2 2 2
1 1 3 4

样例输出

样例输出1

2
4
20
3

样例输出2

2
0
2

数据范围与提示

样例说明

对于样例数据1：
一开始那棵树长这个样：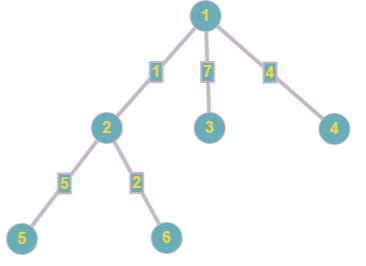

第一个询问最后的答案就是：$\left\lfloor \frac{\left\lfloor \frac{17}{4} \right\rfloor}{2} \right\rfloor=2$
第三条边改变之后，树变成了这样：

第二个询问的答案就是：$\left\lfloor \frac{\left\lfloor \frac{17}{2} \right\rfloor}{2} \right\rfloor=4$
第三个询问中起点和终点一样，故答案为$20$
改了第四条边之后，树变成了这样：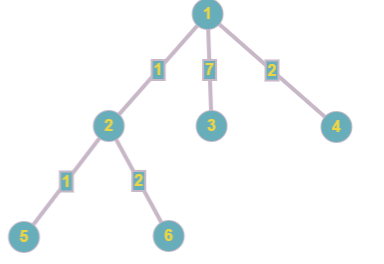

最后一个询问答案就是$\left\lfloor \frac{\left\lfloor \frac{3}{1} \right\rfloor}{1} \right\rfloor=3$

数据范围

对于$70 \%$的数据保证$1 \leqslant n \leqslant 10^3$
对于$100 \%$的数据保证$1 \leqslant n \leqslant 10^5,1 \leqslant c_i \leqslant 10^{18}$
保证每次修改后的边权小于等于原来的边权且不会小于$1$

题解

因为我不知道$q$的范围，所以，我还是尽量让时间复杂度变小了太怂了
所以我进行了两个优化：

1. 边权是$1$的边就不操作了
2. 当两个点的距离$\geqslant 62$时，答案一定是$0$（因为$c\leqslant 10^{18}\leqslant 2305843009213693952=2^{61}\leqslant$所有这两个点之间的路径的点权的乘积）

所以，我们可以用一个并查集把所有连续的、边权是$1$的点全部并到一个集合里，然后直接暴力向上跳就可以了
附上代码：

#include<cstdio>
struct ppap
{
    int to,nxt;
    long long ver;
}e[200010];
int n,q,tot,head[100010],fa[100010],dep[100010],Fa[100010];
long long b[100010],b1[100010],b2[100010];
void add(int u,int v,long long w)
{
    e[++tot].nxt=head[u],head[u]=tot,e[tot].ver=w,e[tot].to=v;
}
void dfs(int x)
{
    for(int i=head[x];i;i=e[i].nxt) if(!fa[e[i].to]) fa[e[i].to]=x,b[e[i].to]=e[i].ver,dep[e[i].to]=dep[x]+1,dfs(e[i].to);
}
int find(int x)
{
    return Fa[x]==x?x:Fa[x]=find(Fa[x]); 
}
int main()
{
    freopen("walk.in","r",stdin);
    freopen("walk.out","w",stdout);
    scanf("%d%d",&n,&q);
    for(int i=1,x,y;i<n;i++){
        long long z;
        scanf("%d%d%lld",&x,&y,&z),add(x,y,z),add(y,x,z);
    }
    fa[1]=1,dfs(1);
    for(int i=1;i<=n;i++) Fa[i]=i;
    for(int i=1,x,y;i<=n;i++) if(b[i]==1) x=find(fa[i]),y=find(i),Fa[y]=x;
    for(int i=1,op,x,y,p,nb1,nb2;i<=q;i++){
        long long v;
        scanf("%d",&op);
        if(op==1){
            scanf("%d%d%lld",&x,&y,&v),x=find(x),y=find(y),nb1=nb2=0;
            while(x!=y&&nb1+nb2<62)
                if(dep[x]>dep[y]) b1[++nb1]=b[x],x=find(fa[x]);
                else b2[++nb2]=b[y],y=find(fa[y]);
            if(nb1+nb2>=62) printf("0\n");
            else{
                for(int i=1;i<=nb1;i++) v/=b1[i];
                for(int i=nb2;i>=1;i--) v/=b2[i];
                printf("%lld\n",v);
            }
        }
        else{
            scanf("%d%lld",&p,&v),p<<=1,y=e[p].to,x=fa[y];
            if(fa[e[p-1].to]==y) p--,y=e[p].to,x=fa[y];
            b[y]=v;
            if(!(b[y]^1)) x=find(x),y=find(y),Fa[y]=x;
        }
    }
}