学好数理化，走遍天下都不怕

DTOJ3123 最大割cut

发表于 更新于 分类于

题目

题目描述

考虑一张$n$个点的边带权无向图，点从$1\sim n$编号
对于图中的任意一个点集(可以为空集或是全集），称所有那些恰好有一个端点在这个点集中的边所组成的边集为割
我们再定义一个割的权值为：这个割中所含的所有边边权的异或和
现在初始时给定一张n个点的空图，接下来会有若干次加（无向）边操作，每次加边后请你求出当前图中权值最大的割的权值

输入格式

第一行两个整数$n,m$表示图的点数与加入的总边数
接下来$m$行每行三个正整数$x,y,w$表示加入一条连接$(x,y)$的权值为w的边
$x,y$可能相同，两点之间可能会有多条边
$w$将以二进制形式从高位向低位给出

输出格式

输出$m$行，按顺序给出每次加边后当前图中权值最大的割的权值
权值也要以二进制形式输出，形式与输入格式中描述的一致

样例

样例输入

1
2
3
4
5
6
7
3 6
1 2 1
1 2 1
3 3 111
1 3 101101
1 2 1011
2 3 111011

样例输出

1
2
3
4
5
6
1
0
0
101101
101101
110000

数据范围与提示

设$l=\log_2{w}$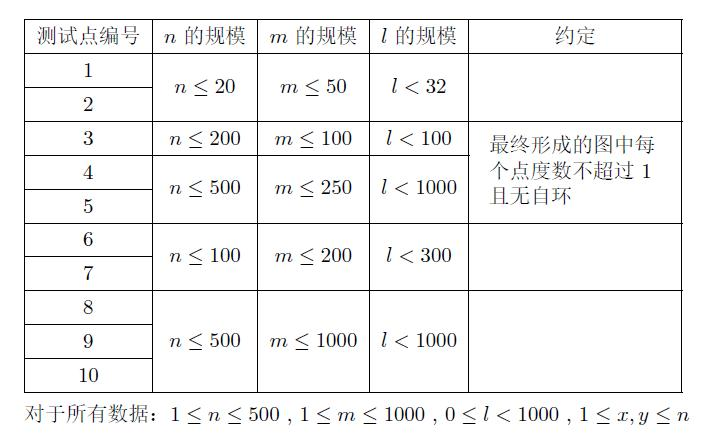
在这里插入图片描述

题解

异或有一个神奇的性质——$a\land a=0$
所以，我们可以把边权转化为点权，点权为所有与这个点相连的边的异或和，对于点集内部的边，异或后就消掉了（因为是无向图），剩下的自然就是割的异或和了
所以我们可以线性基来计算
但是这题有一个很恶心的点——每加一个点就要重新算一遍线性基，如果暴力修改，就算用bitset效率也只有$\Theta(nl^3)$
所以我们可以以时间为下标，用线段树分治求答案
叶子节点求答案，非叶子节点将权值加入线性基
注意：线段树中的bitset必须使用vector，不然就会像我一样，明明对了，却MLE了……
附上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include<cstring>
#include<cstdio>
#include<bitset>
#include<vector>
using namespace std;
bitset<1001> Add,ans,ver[501],xxj[1001];
vector<bitset<1001> > st[4001];
int n,m,top1,top2,z1[1001],z2[1001],v[1001],lst[501];
char s[1001];
int add()
{
    for(int i=1000;i>=0;i--) if(Add[i]){
        if(!v[i]){v[i]=1,xxj[i]=Add;return i;}
        else Add=Add^xxj[i];
    }
    return -1;
}
int pd()
{
    for(int i=1000;i>=0;i--){
        if(Add[i]==1&&ans[i]!=1) return 1;
        if(Add[i]!=1&&ans[i]==1) return 0;
    }
    return 0;
}
void print()
{
    ans.reset();
    for(int i=1000;i>=0;i--)if(v[i]){
        Add=ans^xxj[i];
        if(pd()) ans=Add;
    }
    int flag=0;
    for(int i=1000;i>=0;i--){
        if(!ans[i]&&flag) printf("0");
        else if(ans[i]) printf("1"),flag=1;
    }
    if(!flag) printf("0");
    printf("\n");
}
void change(int p,int l,int r,int L,int R)
{
    if(l==L&&r==R){st[p].push_back(Add);return;}
    int mid=(l+r)/2;
    if(R<=mid) change(p*2,l,mid,L,R);
    else if(mid+1<=L) change(p*2+1,mid+1,r,L,R);
    else change(p*2,l,mid,L,mid),change(p*2+1,mid+1,r,mid+1,R);
}
void ask(int p,int l,int r)
{
    int len=st[p].size();
    for(int i=0;i<len;i++){
        Add=st[p][i];
        int temp=add();
        if(temp!=-1) z2[++top2]=temp;
    }
    z1[++top1]=top2;
    if(l==r){
        print();
        int ls=z1[--top1];
        while(top2!=ls) v[z2[top2--]]=0;
        return;
    }
    int mid=(l+r)/2;
    ask(p*2,l,mid);
    ask(p*2+1,mid+1,r);
    int ls=z1[--top1];
    while(top2!=ls) v[z2[top2--]]=0;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1,x,y,ns;i<=m;i++){
        scanf("%d%d %s",&x,&y,s),ns=strlen(s);
        if(x==y) continue;
        ans.reset();
        for(int j=ns-1;j>=0;j--) ans[ns-j-1]=s[j]-'0';
        if(!lst[x]) ver[x]=ans,lst[x]=i;
        else Add=ver[x],change(1,1,m,lst[x],i-1),ver[x]^=ans,lst[x]=i;
        if(!lst[y]) ver[y]=ans,lst[y]=i;
        else Add=ver[y],change(1,1,m,lst[y],i-1),ver[y]^=ans,lst[y]=i;
    }
    for(int i=1;i<=n;i++) if(lst[i]) Add=ver[i],change(1,1,m,lst[i],m);
    ask(1,1,m);
}