一些概念
在学习重链剖分前,首先要明白以下几个概念:
中二重儿子:就是一个节点的儿子中最“重”的那个,“重”表示的是子树大小最大,如果都一样大,就随便选一个就好了(用$son$数组存储)亲轻儿子:除了重儿子外其他的儿子- 重边:重儿子和父亲之间的边
- 轻边:轻儿子和父亲之间的边
- 重链:重边连在一起形成的链
- 轻链:轻边连在一起形成的链(貌似没啥用)
- 重链顶点:一条重链中,深度最小的点(用$top$数组记录)
为了方便大家理解,这里我画了一张图,来表示重链剖分后的结果: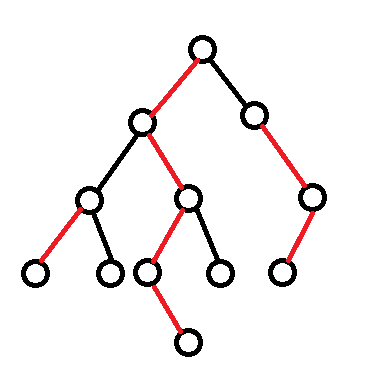
其中,红色的线表示重边,连在一起,形成$3$条重链;黑色的线表示轻边,连在一起,形成$3$条轻链
这样,大家对这些概念应该都了解了吧?
算法讲解
接下来,我们来介绍如何进行重链剖分
首先,我们进行第一遍dfs,求出子树的大小($siz$),重儿子($son$),父亲节点($fa$)和每个点的深度($dep$)
$size$、$fa$和$dep$的求法就不用说了吧……
我们来讲讲$son$的求法
首先,设一个变量$maxson$,初值为$-1$,记录最大的子树大小
接着,对于枚举的每棵子树,假设当前枚举的子树的根为$v$,判断$maxson$和$siz[v]$的大小
如果$siz[v]>maxson$,那么$son[u]=v$
代码:1
2
3
4
5
6
7
8
9
10int dfs1(int x,int Fa,int Dep)
{
dep[x]=Dep,fa[x]=Fa,siz[x]=1;
int maxson=-1;
for(int i=head[x];i!=-1;i=e[i].nxt) if(e[i].v!=Fa){
siz[x]+=dfs1(e[i].v,x,Dep+1);
if(siz[e[i].v]>maxson) maxson=siz[e[i].v],son[x]=e[i].v;
}
return siz[x];
}
接着,我们来讲一讲第二个dfs,这个dfs要求出dfs序($dfn$)和重链顶点($top$)
为了方便,我们首先先遍历重儿子,再遍历其他轻儿子,重儿子的重链顶点和该节点的重链顶点相同,轻儿子的重链顶点是自己
至于方便在什么地方,后面再说
代码:1
2
3
4
5
6
7void dfs2(int x,int Top)
{
dfn[x]=++cnt,top[x]=Top;
if(!son[x]) return;
dfs2(son[x],Top);
for(int i=head[x];i!=-1;i=e[i].nxt) if(!dfn[e[i].v]) dfs2(e[i].v,e[i].v);
}
这样,我们就完成了重链剖分的全过程
应用
那么,剖分完后又有什么好处呢?
求最近公共祖先
众所周知,有一种求最近公共祖先(LCA)的算法,使用的是倍增,这个算法预处理是$\Theta(nlogn)$的,单次询问是$\Theta(logn)$的
有比这个更快的算法吗?有!用重链剖分解决!
等等,这和重链剖分有什么关系呢?最近公共祖先和这两个点所在的重链也不一定一样啊,这怎么做呢?
别急,马上大家就会理解了
我们以下面这张图为例,求两个蓝色的点的最近公共祖先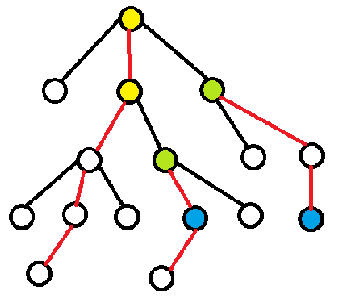
模仿倍增法求LCA,我们就很容易理解重链剖分求LCA的方法了
我们只需要选择深度较深的点,不断向上跳到重链的顶端即可
首先,蓝色的点调到重链顶端(绿点),然后再向上跳一条边(黄点),这样就转换到了另外一条重链上
最后,当两个点在同一条重链上时,深度较小的那个点就是他们的最近公共祖先了
那么,重链剖分求LCA时,预处理为$\Theta(n)$,单次询问为$\Theta(logn)$
完整代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
using namespace std;
struct ppap
{
int u,v,nxt;
}e[2000010];
int n,m,root,tot,cnt,head[2000010],dep[2000010],fa[2000010],son[2000010],siz[2000010],top[2000010],dfn[2000010];
void add(int x,int y)
{
e[++tot].nxt=head[x],head[x]=tot,e[tot].u=x,e[tot].v=y;
}
int dfs1(int x,int Fa,int Dep)
{
dep[x]=Dep,fa[x]=Fa,siz[x]=1;
int maxson=-1;
for(int i=head[x];i!=-1;i=e[i].nxt) if(e[i].v!=Fa){
siz[x]+=dfs1(e[i].v,x,Dep+1);
if(siz[e[i].v]>maxson) maxson=siz[e[i].v],son[x]=e[i].v;
}
return siz[x];
}
void dfs2(int x,int Top)
{
dfn[x]=++cnt,top[x]=Top;
if(!son[x]) return;
dfs2(son[x],Top);
for(int i=head[x];i!=-1;i=e[i].nxt) if(!dfn[e[i].v]) dfs2(e[i].v,e[i].v);
}
int LCA(int x,int y)
{
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(dep[x]>dep[y]) return y;
return x;
}
int main()
{
memset(head,-1,sizeof(head));
cin>>n>>m>>root;
for(int i=1,x,y;i<=n-1;i++) cin>>x>>y,add(x,y),add(y,x);
dfs1(root,0,1),dfs2(root,root);
while(m--){
int x,y;
cin>>x>>y;
cout<<LCA(x,y)<<endl;
}
}
对树上的一条链进行修改和查询
重链剖分还有什么作用呢?
它可以对树上的任意一条链进行修改
以下图为例,我们假设每个点有一个点权,我们要让两个蓝点之间的链上的每个点的权$+1$(包括两个蓝点),怎么操作呢?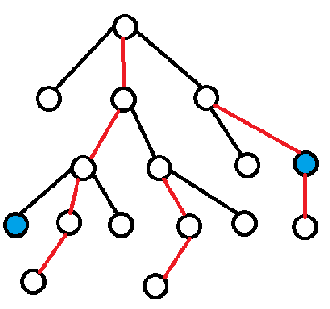
首先,对于这种相连的东西一起修改的题目,我们很容易就会想到线段树
在树上建线段树,用的一定就是dfs序了
还记得我们前面遍历每个节点的子节点时,是先遍历它的重儿子吗?
当时我说这是为了方便
是的,就是在建线段树和计算时更方便了!
因为所有重链上的点的dfs序一定是连续的,这样,一条重链上的点的值修改只需要进行简单的线段树上区间修改即可
所以我们考虑把链划分成许多个重链相连(如下图)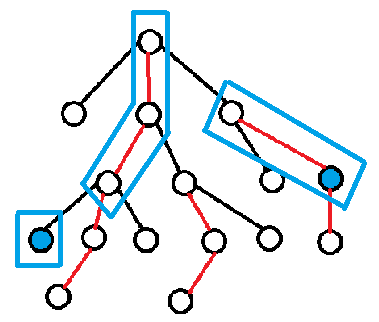
那么,我们就可以分别修改每一段的值,查询时也一样,分别查询每一段的值,然后再加在一起即可
对于这个链的划分操作,和LCA的求法类似,只需要不断地跳到重链顶点的父亲节点,就可以了
模板题代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
using namespace std;
struct ppap
{
int u,v,nxt;
}e[2000010];
struct Segment_Tree
{
int l,r,sum,siz,add;
}t[2000010];
int n,m,root,MOD,tot,cnt,a[2000010],b[2000010],head[2000010],dep[2000010],fa[2000010],son[2000010],siz[2000010],top[2000010],dfn[2000010];
void add(int x,int y)
{
e[++tot].nxt=head[x],head[x]=tot,e[tot].u=x,e[tot].v=y;
}
int dfs1(int x,int Fa,int Dep)
{
dep[x]=Dep,fa[x]=Fa,siz[x]=1;
int maxson=-1;
for(int i=head[x];i!=-1;i=e[i].nxt) if(e[i].v!=Fa){
siz[x]+=dfs1(e[i].v,x,Dep+1);
if(siz[e[i].v]>maxson) maxson=siz[e[i].v],son[x]=e[i].v;
}
return siz[x];
}
void dfs2(int x,int Top)
{
dfn[x]=++cnt,a[cnt]=b[x],top[x]=Top;
if(!son[x]) return;
dfs2(son[x],Top);
for(int i=head[x];i!=-1;i=e[i].nxt) if(!dfn[e[i].v]) dfs2(e[i].v,e[i].v);
}
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r,t[p].siz=r-l+1;
if(l==r){t[p].sum=a[l];return;}
int mid=(l+r)>>1;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
t[p].sum=(t[p*2].sum+t[p*2+1].sum+MOD)%MOD;
}
void spread(int p)
{
if(t[p].add){
t[p*2].sum=(t[p*2].sum+t[p*2].siz*t[p].add)%MOD;
t[p*2+1].sum=(t[p*2+1].sum+t[p*2+1].siz*t[p].add)%MOD;
t[p*2].add=(t[p*2].add+t[p].add)%MOD;
t[p*2+1].add=(t[p*2+1].add+t[p].add)%MOD;
t[p].add=0;
}
}
void change(int p,int l,int r,int d)
{
if(l<=t[p].l&&t[p].r<=r){t[p].sum+=t[p].siz*d,t[p].add+=d;return;}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) change(p*2,l,r,d);
if(r>mid) change(p*2+1,l,r,d);
t[p].sum=(t[p*2].sum+t[p*2+1].sum+MOD)%MOD;
}
int ask(int p,int l,int r)
{
int ans=0;
if(l<=t[p].l&&t[p].r<=r) return t[p].sum;
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) ans=(ans+ask(p*2,l,r))%MOD;
if(r>mid) ans=(ans+ask(p*2+1,l,r))%MOD;
return ans;
}
void modify(int x,int y,int d)
{
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
change(1,dfn[top[x]],dfn[x],d);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
change(1,dfn[x],dfn[y],d);
}
void query(int x,int y)
{
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans=(ans+ask(1,dfn[top[x]],dfn[x]))%MOD;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ans=(ans+ask(1,dfn[x],dfn[y]))%MOD;
cout<<ans<<endl;
}
int main()
{
memset(head,-1,sizeof(head));
cin>>n>>m>>root>>MOD;
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1,x,y;i<=n-1;i++) cin>>x>>y,add(x,y),add(y,x);
dfs1(root,0,1),dfs2(root,root),build(1,1,n);
while(m--){
int op,x,y,z;
cin>>op;
if(op==1) cin>>x>>y>>z,z%=MOD,modify(x,y,z);
else if(op==2) cin>>x>>y,query(x,y);
else if(op==3) cin>>x>>z,change(1,dfn[x],dfn[x]+siz[x]-1,z%MOD);
else if(op==4) cin>>x,cout<<ask(1,dfn[x],dfn[x]+siz[x]-1)<<endl;
}
}
相关练习题
- 洛谷P4315 月下“毛景树”
- 洛谷P2146 [NOI2015]软件包管理器 题解
- 洛谷P4949 最短距离
- 其他需要用到LCA的题目,都可以使用重链剖分求,这里就不列举了