定义
第一类斯特林数
将$n$个元素分成$m$个无标号的轮换$\begin{bmatrix}n\\m\end{bmatrix}$
什么叫轮换?
就是把一堆数放在一个圈上,如果可以通过旋转使得圈上的每个位置上数都和另一个圈上的数是相等的,那么这两个圈等价(意思就是它们是同一个轮换)
比如,现在有三个轮换:
第一个轮换和第二个轮换是等价的,第一个和第三个轮换不是等价的
那么,什么叫无标号的轮换?
就是如果一堆轮换调换顺序后和另一堆轮换完全相同(所有对应的轮换等价),那么这两堆轮换就是等价的
比如,现在有两堆轮换: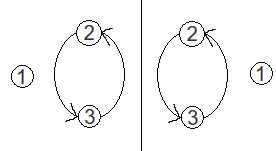
第一堆轮换和第二堆轮换完全相同,是等价的
为了让大家更了解第一类斯特林数,我们举一个例子:$\begin{bmatrix}3\\2\end{bmatrix}=3$
三种方法如下: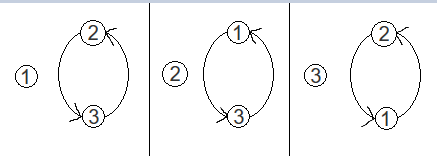
第一类斯特林数还有另一种定义,就是$\prod \limits_{i=0}^{n-1}(x-i)$的$m$次项系数叫$\begin{bmatrix}n\\m\end{bmatrix}$
第二类斯特林数
将$n$个元素分成$m$个无标号的集合$\begin{Bmatrix}n\\m\end{Bmatrix}$
上面我们已经解释过了无标号的意思,相信大家都知道无标号集合的意思了
为了让大家更了解第一类斯特林数,我们举一个例子:$\begin{Bmatrix}3\\2\end{Bmatrix}=3$
三种方法如下:
- $\{\{1\},\{2,3\}\}$
- $\{\{2\},\{1,3\}\}$
- $\{\{3\},\{1,2\}\}$
性质
通项
第一类斯特林数貌似没有通项公式(或者是没用或者我太菜了不知道)
第二类斯特林数的通项为$\begin{Bmatrix}n\\m\end{Bmatrix}=\frac{1}{m^2}\sum \limits_{i=0}^m(-1)^i\binom{m}{k}(m-i)^n$貌似也没什么用……我不会证……记住就好了我好像也记不住???递推
第一类斯特林数
$\begin{bmatrix}n\\m\end{bmatrix}=(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}+\begin{bmatrix}n-1\\m-1\end{bmatrix}$
证明:假如$n-1$个元素构成了$m-1$个无标号的轮换,第$n$个元素独自构成一个无标号的轮换,有$\begin{bmatrix}n-1\\m-1\end{bmatrix}$种方法。如果$n-1$个元素构成了$m$个无标号的轮换,将第$n$个元素插入到任意元素的左边,有$(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$种方法
$\therefore \begin{bmatrix}n\\m\end{bmatrix}=(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}+\begin{bmatrix}n-1\\m-1\end{bmatrix}$第二类斯特林数
$\begin{Bmatrix}n\\m\end{Bmatrix}=m\begin{Bmatrix}n-1\\m\end{Bmatrix}+\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$
证明:假如$n-1$个元素构成了$m-1$个无标号的集合,第$n$个元素独自构成一个无标号的集合,有$\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$种方法。如果$n-1$个元素构成了$m$个集合,将第$n$个元素插入到任意集合中,有$m\begin{Bmatrix}n-1\\m\end{Bmatrix}$种方法
$\therefore \begin{Bmatrix}n\\m\end{Bmatrix}=m\begin{Bmatrix}n-1\\m\end{Bmatrix}+\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$特殊值
第一类斯特林数
$\begin{bmatrix}n\\0\end{bmatrix}=0,\begin{bmatrix}n\\1\end{bmatrix}=1,\begin{bmatrix}n\\n-1\end{bmatrix}=\binom{n}{2},\begin{bmatrix}n\\n\end{bmatrix}=1$
自己想吧,太简单了,不证了第二类斯特林数
$\begin{Bmatrix}n\\0\end{Bmatrix}=0,\begin{Bmatrix}n\\1\end{Bmatrix}=1,\begin{Bmatrix}n\\n-1\end{Bmatrix}=\binom{n}{2},\begin{Bmatrix}n\\n\end{Bmatrix}=1$
自己想吧,太简单了,不证了快速幂???
①$n^m=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}$
其中$n^{\underline{i}}$表示$n$的$i$次下降幂,即$n^{\underline{i}}=\prod \limits_{k=0}^{i-1}(n-k)$
证明:
当$m=1$时,$\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}=\begin{Bmatrix}1\\1\end{Bmatrix} n=n$
假设$m=k$时成立
当$m=k+1$时,$n^{k+1}=n\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix} n^{\underline{i}}=\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix}\left( n^{\underline{i+1}}+in^{\underline{i}}\right)=\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix} n^{\underline{i+1}}+\sum \limits_{i=0}^{k} \begin{Bmatrix}k\\i\end{Bmatrix} in^{\underline{i}}=\sum \limits_{i=0}^{k+1} \begin{Bmatrix}k\\i-1\end{Bmatrix} n^{\underline{i}}+\sum \limits_{i=0}^{k+1} \begin{Bmatrix}k\\i\end{Bmatrix} in^{\underline{i}}=\sum \limits_{i=0}^{k+1} \left(\begin{Bmatrix}k\\i-1\end{Bmatrix}+i\begin{Bmatrix}k\\i\end{Bmatrix}\right) n^{\underline{i}}=\sum \limits_{i=0}^{k+1} \begin{Bmatrix}k+1\\i\end{Bmatrix} n^{\underline{i}}$
$\therefore n^m=\sum \limits_{i=0}^{m} \begin{Bmatrix}m\\i\end{Bmatrix} n^{\underline{i}}$
②$n^{\overline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} n^i$
其中$n^{\overline{m}}$表示$n$的$i$次上升幂,即$n^{\overline{m}}=\prod \limits_{i=0}^{m-1}(n+i)$
证明:
当$m=1$时,$\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} n^i=\begin{bmatrix}1\\1\end{bmatrix} n=n$
假设$m=k$时成立
当$m=k+1$时,$n^{\overline{k+1}}=(n+k)n^{\overline{k}}=n\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} n^i+k\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k\\i-1\end{bmatrix} n^i+\sum \limits_{i=0}^{k+1} k\begin{bmatrix}k\\i\end{bmatrix} n^i=\sum \limits_{i=0}^{k+1} \left(\begin{bmatrix}k\\i-1\end{bmatrix}+k\begin{bmatrix}k\\i\end{bmatrix}\right) n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k+1\\i\end{bmatrix} n^i$
$\therefore n^{\overline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} n^i$
③$n^{\underline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} (-1)^{m-i} n^i$
证明:
当$m=1$时,$\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} (-1)^{m-i} n^i=\begin{bmatrix}1\\1\end{bmatrix} n=n$
假设$m=k$时成立
当$m=k+1$时,$n^{\underline{k+1}}=(n-k)n^{\underline{k}}=n\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} (-1)^{k-i} n^i-k\sum \limits_{i=0}^{k} \begin{bmatrix}k\\i\end{bmatrix} (-1)^{k-i} n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k\\i-1\end{bmatrix} (-1)^{k+1-i} n^i+\sum \limits_{i=0}^{k+1} k\begin{bmatrix}k\\i\end{bmatrix} (-1)^{k+1-i} n^i=\sum \limits_{i=0}^{k+1} \left(\begin{bmatrix}k\\i-1\end{bmatrix}+k\begin{bmatrix}k\\i\end{bmatrix}\right) (-1)^{k+1-i} n^i=\sum \limits_{i=0}^{k+1} \begin{bmatrix}k+1\\i\end{bmatrix} (-1)^{k+1-i} n^i$
$\therefore n^{\underline{m}}=\sum \limits_{i=0}^{m} \begin{bmatrix}m\\i\end{bmatrix} (-1)^{m-i} n^i$斯特林反演
若$f(n)=\sum \limits_{i=1}^n\begin{Bmatrix}n\\i\end{Bmatrix}g(i)$,则$g(n)=\sum \limits_{i=1}^n(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}f(i)$
这个$-1$的次数怎么这么熟?
是的,这就是上面的③式中$-1$次数
可以用斯特林反演说明①式和③式是等价的
但是这玩意儿好像没啥用,至少我没用过我就没做过几道斯特林数的题目,所以我也不会证……
ps:定义部分从百度百科上的内容删改而成