题目

题目描述

“我有个愿望，我希望穿越一切找到你”
这是个二维平面世界，平面上有$n$个特殊的果实，我从$(0,0)$点出发，希望得到尽量多的果实，但是出于某种特殊的原因，我的运动方式只有三种（假设当前我在$(x,y)$）：

我可以走到$(x+1,y)$
我可以走到$(x,y+1)$
我可以走到$(x+1,y+1)$

现在我需要你的帮助，帮我找出我最多能够得到多少个果实

输入格式

第一行一个整数$n$表示有多少个被标记的点
接下来$n$行每行两个整数$x,y$表示一个点的坐标

输出格式

一行一个整数表示答案，表示我最多能够得到多少个果实

样例

样例输入

样例输出

数据范围与提示

样例说明

样例输入的点如图所示：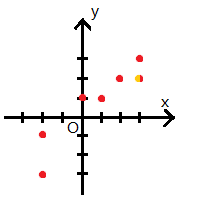

数据范围

对于$70 \%$的数据$1 \leqslant n \leqslant 10^3$
对于$100 \%$的数据$1 \leqslant n \leqslant 10^5,-10^9 \leqslant x,y \leqslant 10^9$

题解

显然，只有在第一象限、$x$轴和$y$轴的正半轴或者原点上的点可以到达
所以去掉不是第一象限、$x$轴和$y$轴的正半轴或者原点上的点，把剩下的点按照$x$坐标排序，求$y$坐标的最长上升子序列即可
附上代码：

#include<algorithm>
#include<cstdio>
using namespace std;
struct ppap
{
    int x,y;
}a[100010];
int n,len,ans,lcs[100010];
int cmp(const ppap &a,const ppap &b)
{
    return a.y<b.y;
}
int main()
{
    scanf("%d",&n);
    for(int i=1,x,y;i<=n;i++){
        scanf("%d%d",&x,&y);
        if(x<0||y<0) continue;
        a[++len].x=x,a[len].y=y;
    }
    sort(a+1,a+1+len,cmp);
    for(int i=1;i<=len;i++){
        if(a[i].x>=lcs[ans]) lcs[++ans]=a[i].x;
        else{
            int temp=lower_bound(lcs+1,lcs+1+ans,a[i].x)-lcs;
            lcs[temp]=a[i].x;
        }
    }
    printf("%d",ans);
}