题目

题目描述

英文题目

There is a cake placed in a labyrinth and you desperately want to eat it. You have a map of the labyrinth, which is a grid of R rows and C columns. Each grid cell contains one of the following characters:

(number sign) which denotes a wall block,
. (dot) which denotes an open square,
S (uppercase letter s) which denotes an open square of your current location,
C (uppercase letter c) which denotes an open square with the cake.

You may only walk on the open squares and move from one open square to another if they share a side. Additionally, the rectangular area depicted on the map is completely surrounded by wall blocks.
In order to reach the cake faster you have acquired a portal gun from Aperture ScienceTM, which operates as follows. At any time it can fire a portal in one of the four directions up,left, down and right. When a portal is fired in some direction, it will fly in that direction until it reaches the first wall. When this happens, a portal will be spawned on the wall block, on the side that faces you.
At most two portals can exist at any given time. If two portals are already placed in the labyrinth, then one of them (selected by you) will be removed immediately upon using the portal gun again. Firing a portal at an existing portal will replace it (there may be at most one portal per side of wall block). Note that there may be two portals placed on different sides of the same wall block.
Once two portals are placed in the labyrinth you can use them to teleport yourself. When standing next to one of the portals, you can walk into it and end up at the open square next to the other portal. Doing this takes as much time as moving between two adjacent squares.You may assume that firing portals does not take time and moving between two adjacent squares or teleporting through portals takes one unit of time.
Task
Given the map of the labyrinth together with your starting location and the location of the cake, calculate the minimum possible time needed for you to reach the cake.

中文翻译

给出一张四连通的网格图，#代表墙，.代表空地，S代表出发点，C代表目的地，地图四周都是墙,求S到C的最短路
走的时候可以向上下左右中的某个方向发射奇怪的东西(portals)，portals会贴在发射方向的墙上
地图上只允许同时存在两个portals，如果已经发射了两个再发射第三个，那么你需要在之前的那两个中的选一个使它消失
两个portals可以存在于一块墙的两面，但不能存在于一块墙的同面
当你身边是墙且那块墙上有面向你的portals时，你可以走进那个portals，从另一个portals出来
相邻两点距离为$1$，走portals距离也为$1$

输入格式

第一行2个数$R,C$，表示矩形的长和宽
接下来$R$行，每行一个长为$C$的字符串，表示这张图

输出格式

输出一行表示答案

样例

样例输入

4 4
.#.C
.#.#
....
S...

样例输出

数据范围与提示

样例解释

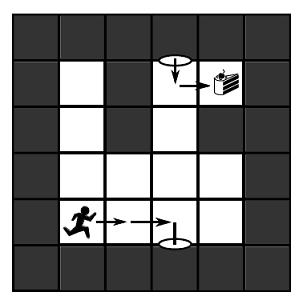
One quickest sequence of moves is as follows:

move right,
move right, shootone portal up, and one portal down,
move through the bottom portal,

moveone square right and reach the cake.

数据范围

Subtask $1$ ($11$ points): $1 \leqslant R \leqslant 10, 1 \leqslant C \leqslant 10$.
Subtask $2$ ($20$ points): $1 \leqslant R \leqslant 50, 1 \leqslant C \leqslant 50$.
Subtask $3$ ($20$ points): $1 \leqslant R \leqslant 200, 1 \leqslant C \leqslant 200$. Every open square has at least one wall block adjacent to it.
Subtask $4$ ($19$ points): $1 \leqslant R \leqslant 200, 1 \leqslant C \leqslant 200$.
Subtask $5$ ($30$ points): $1 \leqslant R \leqslant 1000, 1 \leqslant C \leqslant 1000$.

题解

因为所有的传送门都只能放在墙前面的那一格，所以对于每一个点，我们可以预处理出每个点四个方向最远的不是墙的点（就是最近的墙的前面一格）和到这个点的距离的最小值$w_{i,j}$
那么，移动的时候就考虑放传送门，就是走到四个方向的最远点，距离就是$w_{i,j}+1$（有点类似于Dijkstra算法）
附上代码：

#include<cstring>
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
struct ppap
{
    int x,y;
};
queue<ppap> q;
int n,m,sx,sy,ex,ey,w[1010][1010][5],d[1010][1010],flag[1010][1010],dis[1010][1010],v[1010][1010];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
char map[1010][1010];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){
        scanf(" %c",&map[i][j]);
        if(map[i][j]=='S') sx=i,sy=j;
        if(map[i][j]=='C') ex=i,ey=j;
    }
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){
        w[i][j][0]=w[i-1][j][0]+1,w[i][j][3]=w[i][j-1][3]+1;
        if(map[i][j]=='#') q.push((ppap){i,j}),w[i][j][0]=w[i][j][3]=d[i][j]=-1,flag[i][j]=1;
        else{
            if(i==1) w[i][j][0]=0;
            if(j==1) w[i][j][3]=0;
        }
    }
    for(int i=n;i;i--) for(int j=m;j;j--){
        w[i][j][1]=w[i][j+1][1]+1,w[i][j][2]=w[i+1][j][2]+1;
        if(map[i][j]=='#') q.push((ppap){i,j}),w[i][j][1]=w[i][j][2]=-1;
        else{
            if(i==n) w[i][j][2]=0;
            if(j==m) w[i][j][1]=0;
        }
    }
    for(int i=1;i<m;i++){
        if(map[1][i]=='#') continue;
        q.push((ppap){1,i}),flag[1][i]=1,d[1][i]=0;
    }
    for(int i=2;i<=n;i++){
        if(map[i][1]=='#') continue;
        q.push((ppap){i,1}),flag[i][1]=1,d[i][1]=0;
    }
    for(int i=2;i<=m;i++){
        if(map[n][i]=='#') continue;
        q.push((ppap){n,i}),flag[n][i]=1,d[n][i]=0;
    }
    for(int i=1;i<n;i++){
        if(map[i][m]=='#') continue;
        q.push((ppap){i,m}),flag[i][m]=1,d[i][m]=0;
    }
    while(!q.empty()){
        ppap t=q.front();q.pop();
        for(int i=0,X,Y;i<4;i++){
            X=t.x+dx[i],Y=t.y+dy[i];
            if(X<1||X>n||Y<1||Y>m) continue;
            if(map[X][Y]!='#'&&(!flag[X][Y])){
                d[X][Y]=d[t.x][t.y]+1,q.push((ppap){X,Y}),flag[X][Y]=1;
            }
        }
    }
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) dis[i][j]=0x7fffffff;
    q.push((ppap){sx,sy}),dis[sx][sy]=0;
    while(!q.empty()){
        ppap t=q.front();q.pop();
        v[t.x][t.y]=0;
        for(int i=0,X,Y;i<4;i++){
            X=t.x+dx[i],Y=t.y+dy[i];
            if(map[X][Y]=='#') continue;
            if(dis[X][Y]>dis[t.x][t.y]+1){
                dis[X][Y]=dis[t.x][t.y]+1;
                if(!v[X][Y]) q.push((ppap){X,Y});
                v[X][Y]=1;
            }
        }
        for(int i=0,X,Y;i<4;i++){
            X=t.x+w[t.x][t.y][i]*dx[i],Y=t.y+w[t.x][t.y][i]*dy[i];
            if(w[t.x][t.y][i]>d[t.x][t.y]+1&&dis[X][Y]>dis[t.x][t.y]+d[t.x][t.y]+1){
                dis[X][Y]=dis[t.x][t.y]+d[t.x][t.y]+1;
                if(!v[X][Y]) q.push((ppap){X,Y});
                v[X][Y]=1;
            }
        }
    }
    printf("%d",dis[ex][ey]);
}

题目