题目
题目描述
C 酱有一个$m \times n$的数表,行与列的编号都从$1$开始。令$f_{i,j}$表示表格第$i$行第$j$列内的数,那么对于表格的第$i(i>1)$行有
然而 C 酱已经把表格中的数忘得差不多了,他现在只记得第$p$行的数。他希望你能够帮忙还原出部分位置的数值。
输入格式
输入第一行为$6$个整数$m,n,a,b,p,q$,其中$q$表示询问的个数。
接下来一行共$n$个整数,依次表示$f_{p,1},f_{p,2},\cdots,f_{p,n}$。
接下来$q$行,每行两个整数$x,y$,表示 C 酱询问你$f_{x,y}$的数值。
输出格式
输出共$q$行,依次表示每个询问的答案在模$998244353$意义下的取值。
即设答案可以表示为分式$\frac{a}{b}$ ,则输出整数$x$使得$b \times x \equiv a \pmod {998244353}$且$0 \leqslant x < 998244353$。可以证明这样的整数$x$是唯一的。
样例
样例输入 1
1 | 5 4 1 1 3 5 |
样例输出 1
1 | 2 |
样例输入 2
1 | 10 5 233 2333 6 4 |
样例输出 2
1 | 110343631 |
数据范围与提示
| 测试点编号 | $n$ | $m$ | $a,b$ | $p$ |
|---|---|---|---|---|
| $1,2$ | $\leqslant 100$ | $\leqslant 10^5$ | − | $p=1$ |
| $3,4$ | $\leqslant 100$ | $\leqslant 10^5$ | $a=b=1$ | − |
| $5,6,7,8$ | $\leqslant 100$ | $\leqslant 10^5$ | − | − |
| $9,10,11,12$ | $\leqslant 10^5$ | $\leqslant 10^5$ | − | $p=1$ |
| $13,14,15,16$ | $\leqslant 10^5$ | $\leqslant 10^5$ | − | $p=m$ |
| $17,18,19,20$ | $\leqslant 10^5$ | $\leqslant 10^7$ | − | − |
对于$100\%$的数据,保证$1 \leqslant q \leqslant 100 , 1 \leqslant x , p \leqslant m , 1 \leqslant y \leqslant n , 1 \leqslant a,b < 998244353,0 \leqslant f_{i,j} < 998244353$。
题解
40分算法
暴力把所有格子算出来
代码:
1 |
|
AC算法
我们先分类讨论,在第$p$行下和在第$p$行上
若在第$p$行下,我们可以由上面的两个点得出下面一个点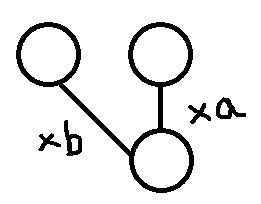
由题目可知,$f_{i,j}=a\times f_{i-1,j}+b\times f_{i-1,j-1}$
所以,我们考虑第$p$行中,要求的点$(x,y)$左侧的点$(p,i)$(即$i\leqslant y$),它对$(x,y)$的贡献就是$(p,i)$到$(x,y)$的路径条数(只能向右下或向下走)$\times a^{\cdots}\times b^{\cdots}$
我们只需要求$(p,i)$到$(x,y)$的路径条数和$a$、$b$的次数
假设$n=x-p,m=y-i$,那么,我们可以知道我们一共需要走$n$步,向右下走$m$步,所以路径数就是$C^m_n$
所以最终的结果就是:$C^m_n\times a^{n-m}\times b^{m}$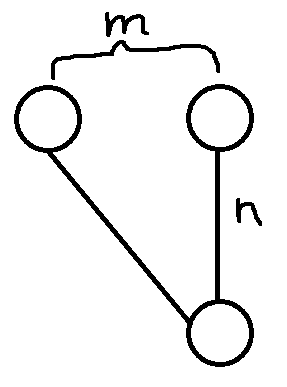
所以我们还能得到一个范围:$n\geqslant m$
终于,我们解决了$(x,y)$在在$p$行下,即$x>p$的情况,接下来,我们讨论一下$x<p$的情况
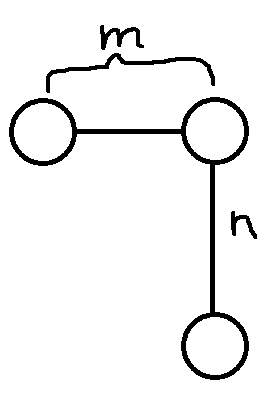
同样,我们可以通过下面的和他左边的点得到这个位置的值,$f_{i,j}=\frac{f_{i+1,j}}{a}-\frac{b\times f_{i,j-1}}{a}$,那么,问题就变成考虑第$p$行中,要求的点$(x,y)$左侧的点$(p,i)$(即$i\leqslant y$),它对$(x,y)$的贡献就是$(p,i)$到$(x,y)$的路径条数(只能向上或右走)$\times a^{\cdots}\times \left(-\frac{b}{a}\right)^{\cdots}$
同样假设$n=p-x,m=y-i$,但是,不一样的地方在于第一步必须向上走!所以,我们可以知道去掉先向上走的一步后,一共需要走$n+m-1$步,向右走$m$步,所以路径数就是$C^m_{n+m-1}$
所以最终的结果就是:$C^m_{n+m-1}\times a^{n}\times \left(-\frac{b}{a}\right)^{m}$
注意事项
- 取模
- 阶乘的逆元可以反着算,$invjc_i=invjc_{i+1}*(i+1)$,这样就避免了多次的$pow$
- 提前保存$a$的逆元
- 提前保存$-\frac{b}{a}$的次方,避免计算$-1^{y-i}$
- $x<p$的情况中,是$C^m_{n+m-1}$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
using namespace std;
int n,m,p,q;
long long a,b,MOD=998244353,f[10100010],jc[10100010],cj[10100010],pa[10100010],pb[10100010],ap[10100010],bp[10100010];
/*
f:第p行的值
jc:阶乘
cj:阶乘的逆元
pa:a的次方
pb:b的次方
ap:pa的逆元
bp:-b/a的次方
*/
long long POW(long long a,long long b)//快速幂
{
long long ans=1;
for(;b;b>>=1){
if(b&1) ans=(ans*a)%MOD;
a=(a*a)%MOD;
}
return ans;
}
long long C(int x,int y)//求组合数
{
if(x<0||y<0||y>x) return 0;
return jc[x]*cj[y]%MOD*cj[x-y]%MOD;
}
int main()
{
cin>>m>>n>>a>>b>>p>>q;
jc[0]=pa[0]=pb[0]=ap[0]=bp[0]=1;
for(int i=1;i<=10100000;i++) jc[i]=jc[i-1]*i%MOD;//暴力求阶乘
cj[10100000]=POW(jc[10100000],MOD-2);
for(int i=10099999;i>=0;i--) cj[i]=cj[i+1]*(i+1)%MOD;//反向求阶乘的逆元
long long na=POW(a,MOD-2),nb=MOD-(b*na%MOD);
for(int i=1;i<=10100000;i++) pa[i]=pa[i-1]*a%MOD,pb[i]=pb[i-1]*b%MOD,ap[i]=ap[i-1]*na%MOD,bp[i]=bp[i-1]*nb%MOD;
for(int i=1;i<=n;i++) cin>>f[i];
for(int i=1,x,y;i<=q;i++){
cin>>x>>y;
if(x==p){cout<<f[y]<<endl;continue;}
long long ans=0;
if(x>p){for(int j=1;j<=y;j++) if(y-j<=x-p) ans=(ans+f[j]*C(x-p,y-j)%MOD*pa[x-y-p+j]%MOD*pb[y-j]%MOD)%MOD;}
//括号很重要!不能删除
else for(int j=1;j<=y;j++) ans=(ans+f[j]*C(y-x+p-j-1,y-j)%MOD*ap[p-x]%MOD*bp[y-j]%MOD)%MOD;
//分类讨论
cout<<ans<<endl;
}
}