1、矢量的定义
矢量是一种既有大小又有方向的量,又称为向量。在计算机中,矢量图可以无限放大永不变形 (反正我没看懂)。——百度百科
2、矢量的表示及其相关量的表示
(1)矢量的表示
矢量可以表示为一个小写字母$a$上面一个箭头$\vec{a}$(ps:正确的箭头应该是$\rightharpoonup$这样的,而不是$\rightarrow$的,但$L_{A}T^{E}X$上打不出来)或者一个粗体 A
在$n$维空间内,矢量通常被表示为一个$n$元组$(a_{1},a_{2},\cdots \cdots,a_{n})$
(2)矢量夹角的表示
两个矢量$\vec{a},\vec{b}$的夹角表示为$\langle\vec{a},\vec{b}\rangle$
3、矢量的运算
(1)矢量的模
即矢量的长度,记为$|\vec{a}|$
(2)矢量的加法
满足三角形法则,如图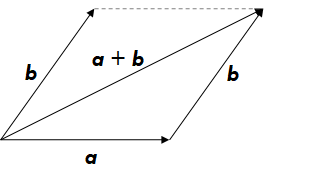
(3)矢量的减法
满足平行四边形法则,如图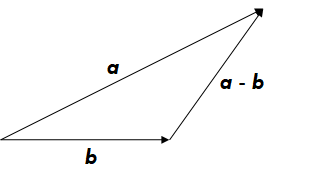
(4)矢量的点乘
两个矢量的点乘是标量,$(a_{1},a_{2},\cdots\cdots,a_{n})\cdot(b_{1},b_{2},\cdots\cdots,b_{n})\overset{\underset{def}{}}{=}\sum \limits_{i=1}^{n}a_{i}b_{i},\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|cos(\langle\vec{a},\vec{b}\rangle)$
这时,我们终于可以给出矢量的模的表达式了$|\vec{a}|\overset{\underset{def}{}}{=}\sqrt{(\vec{a})^2}$
点乘满足交换律和分配律
(5)矢量的叉乘
有$0.999999994538$的概率我们不考虑矢量的叉乘后的结果,我们只考虑矢量的叉乘后矢量的模
$(a_{1},a_{2})\times(b_{1},b_{2})\overset{\underset{def}{}}{=}a_{1}b_{2}-a_{2}b_{1},\vec{a}\times\vec{b}=|\vec{a}||\vec{b}|sin(\langle\vec{a},\vec{b}\rangle)$
矢量的叉乘的本质的有向面积,它的方向满足右手螺旋法则:先把手掌除大拇指以外的$4$个指头展开,指向$\vec{a}$的方向,然后把$4$个指头弯起来,弯的方向由$\vec{a}$转向矢量$\vec{b}$(转的角度须小于$\pi$),此时大拇指立起的方向,就是$\vec{a}\times\vec{b}$的方向。
矢量的叉乘满足逆交换律,即$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$
(6)矢量的极角
向量$\vec{a}$的极角$\theta$为$atan2(y,x)$
4、矢量的变换
(1)缩放
$\vec{a}$方向的单位矢量(即长度为1的矢量)为$\frac{\vec{a}}{|a|}$
与$\vec{a}$同向但长度为$l$的矢量为
(2)平移
平移后的矢量和平移前的矢量是同一个向量
(3)旋转
矢量$\vec{a}=(x,y)$逆时针旋转$\theta$,得到的矢量$\vec{a’}=(xcos\theta-ysin\theta,ycos\theta+xsin\theta)$
(4)投影
矢量$\vec{b}$在矢量$\vec{a}$上的投影为$\vec{a}\frac{\vec{a}\cdot\vec{b}}{\vec{a}^2}$
(5)对称
记矢量$\vec{b}$在矢量$\vec{a}$上的投影为$\vec{c}=\vec{a}\frac{\vec{a}\cdot\vec{b}}{\vec{a}^2}$,则矢量$\vec{b}$关于矢量$\vec{a}$的对称为$\vec{b}-2(\vec{b}-\vec{s})=2\vec{a}\frac{\vec{a}\cdot\vec{b}}{\vec{a}^2}=\vec{b}$